这两天看到《数学之美》中讲到的计算机中的数学模型,以及《What is Mathematics》的数论,看的心痒痒。今天懒癌暂时被抑制住了,我就要分析一下,密码学中的数学模型!
我们依据RSA加密算法的基本特性(也是很多加密算法的共同点):
- 它们都有两个完全不同的样式,一个用于加密,一个用于解密。
- 两个看上去无关的钥匙,在数学上是有联系的。
现在,我们先使用相对简单的RSA算法来表明公钥的原理,并给Vision加密和解密。
首先,先将Vision变成一串数字,以它的ASCII值为例:
$$X=086105115105111110$$(每三位代表一个字母)做明码,针对这个明码来设计一个密码系统。
找两个很大的素数$P$和$Q$,越大越好,比如100位长的,计算他们的乘积(因为越大越难分解)
$N=P\times Q$
$M=(P-1)\times (Q-1)$找一个与$M$互素的整数$E$(互素,$M$与$E$除了1之外没有公约数)
找一个整数$D$,使得$E\times D\ mod\ M=1$ (费马小定理)
费马小定理:如果p是任意一个不能整除整数a的素数,则满足:
$$a^{p-1}\equiv 1(mod\ p)$$
现在这样一个密码系统就已经设计好了。其中$E$是公钥(用于加密),$D$是私钥(用于解密),联系公钥和秘钥的乘积$N$是公开的。
现在我们对要加密的数据进行加密:
$$X^E\ mod\ N=Y$$
加密,完成!现在没有密钥$D$神仙也不能从$Y$中解密出$X$(运算量太大,从$N$中分解出$P$和$Q$就要算上好多年)
可以使用密钥就可以轻而易举地从$Y$中得到$X$
$$Y^D\ mod\ N=X$$
基本流程如下: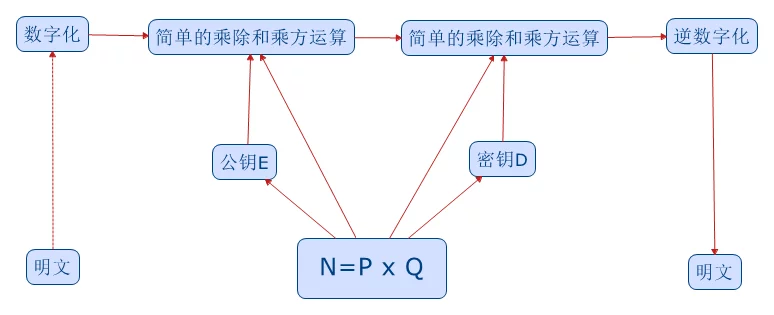
可以看出,公钥加密的好处:
- 简单,就是一些乘除开方。
- 可靠,很难逆向破解,公钥只能用来加密,加密后非密钥不能解密。
- 灵活,可以产生很多公钥和密钥的组合分配给不同的加密者。
世界上没有不能破解的密码,关键是它能保证在多长时间内不被破解。
要破解公钥加密的方式,迄今为止最有效的办法还是分解$N$,通过$N$逆向分解出$P$和$Q$,这也是$N$和$Q$一定要找非常大的素数的原因,因为素数的重要性就在于:每一个整数都能表示为素数的乘积,除了次序可以任意排列外,一个数N的素因子分解是唯一的。意思是要在大数$N$的所有素因子中组合出$P$和$Q$满足$P\times Q=N$,因为选择的$P$和$Q$都是极大的素数,所以,这个计算量是不可估量的,就算由计算机穷举每一种可能性,也要很久,实际上就是再拼计算机的计算速度。
总结:其实加密运算用到的最重要的概念就是素数,这才是加密算法中的根本,在于其难分解性。
其实数学的很多知识都是如此,看起来没有什么大用,但实际上,用处很大,就拿搜索引擎来说吧,究其本质也是布尔运算,但是其中也掺杂了很多技术。
最后一句感叹:数学,学以致用才好!

