使用Gprof分析代码性能瓶颈

使用profiler来分析代码的性能比纯脑补分析起来更省力更详细也更直观。

Gprof是GNU binutils工具之一。可以分析出代码中每个函数的调用次数、每个函数消耗的处理器时间等。

更多的关于gprof的信息可以参照这两篇文章：gprof使用和介绍和Linux性能评测工具之一:gprof篇

在这里就简单说下gprof的用法(更多的参数可以看上面的博文)：

使用G++ 编译代码时需要加-pg参数
编译完成后运行生成的.exe文件，会生成gmon.out文件
导出分析结果:gprof -b runFileName.exe gmon.out>resault.txt

其实为了方便，我在我的Sublime Text的Build System中使用G++编译时就使用了gprof(-pg参数)，关于我Sublime Text的配置可以看这里：配置SublimeText为C/C++的轻量级IDE

下面我们就来实践一下使用gprof分析代码：

就拿输出N以内的素数举例吧。

素数指在大於1的自然数中，除了1和此整数自身外，無法被其他自然数整除的数（也可定義為只有1和本身两个因数的数）。——维基百科

首先我们先写一份代码，由素数的定义可得，最简单的验证一个数N是否为素数的方式是依次让它对2至N-1取余，若2~N-1中存在一个数能够被N整除，所以我们就可以判定它不是素数。

如下代码：

// 求1000以内的所有素数
bool prime(int n){
	for (int i = 2; i < n; ++i){
		if(n%i==0)
			return false;
	}
	return true;
}
int main(void)
{
	int n=1000;
	// 统计N以内素数的个数
  	int index=0;
	for (int i = 2; i < n; ++i){
		if(prime(i)){
			printf("%d\t",i);
          	 ++index;
		}
	}
  	printf("\nThe number of prime numbers within %d to %d\n",n,index);
	return 0;
}

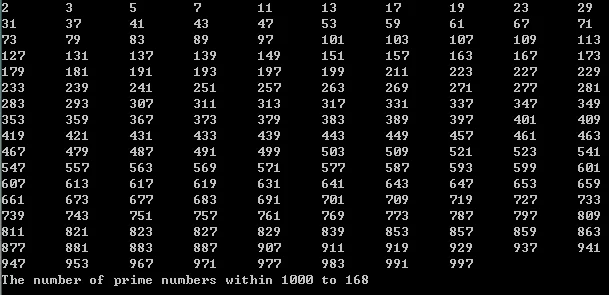
在1000以内共找到了168个素数。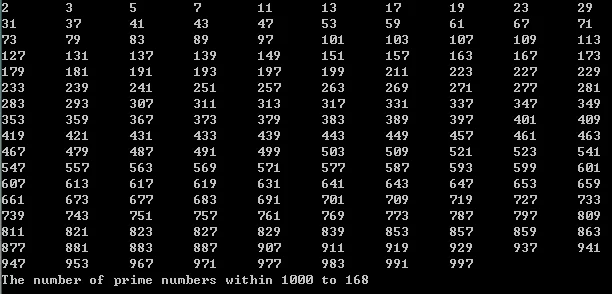

使用gprof来分析一下：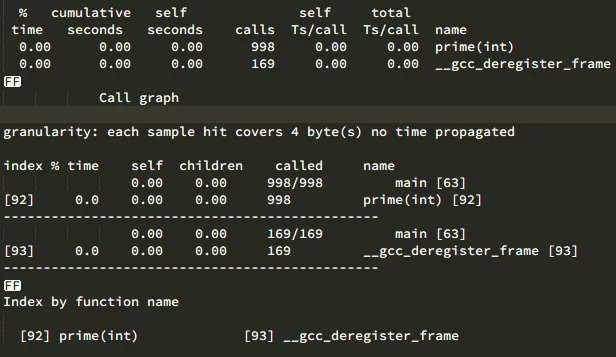

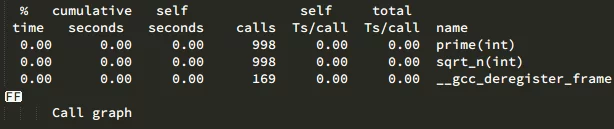
我们可以看到prime被调用了998次(因为是1000以内的数)。

这个算法是非常无脑的穷举(从2~N)，下面我们来优化一下这个算法。

确定性演算法之埃拉托斯特尼筛法(另一种试除法)

尝试从2到$\sqrt{N}$ 的整数是否整除N，来判定N是否为素数。

修改后的代码如下:

int sqrt_n(int n){
	return (int)sqrt((float)n);
}
bool prime(int n){
	for (int i = 2; i <= sqrt_n(n); ++i){
		if(n%i==0)
			return false;
	}
	return true;
}
int main(void)
{
	int n=1000;
	for (int i = 2; i < n; ++i){
		if(prime(i)){
			printf("%d\t",i);
		}
	}
	return 0;
}

同样来用gprof分析一下:

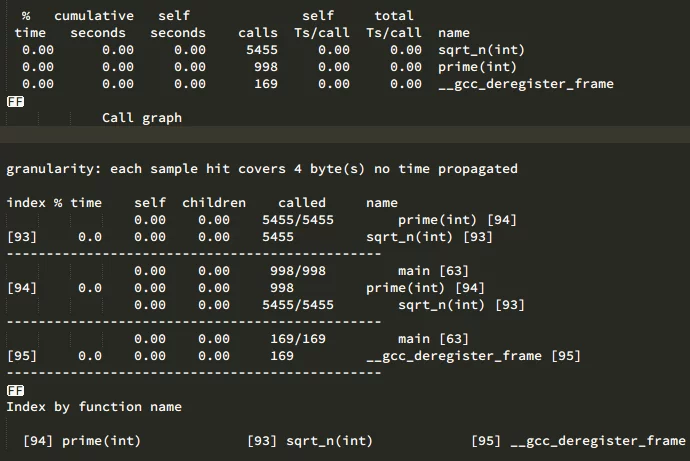
可以看到prime调用了998次，sqrt_n调用了5455次(对n实行了5455次sqrt操作)。

还有特别需要注意的一点是这句代码:

for (int i = 2; i <= sqrt_n(n); ++i)

这个循环每执行一次迭代都会调用一次sqqt_n，造成了prime函数每操作一个N就会调用N次sqrt_n函数，而实际上sqrt_n在prime中的作用只需要执行一次就足够了，所以我们可以修改一下代码：

int tmp=sqrt_n(n)
for (int i = 2; i <= tmp; ++i)

如何再一次优化？

思考一下：我们试除的顺序是这样的：

2 3 4 5 6 7 8 9 10 11 12 13 14……N-1

其中4,6,8,10,12,14…都是2的整数倍，所以我们只需要对N%2就可以替代对这些数字的取余

另外9,15,21,24….都是3的整数倍，所以我们只需要对N%3就可以替代这些数字

对于5的整数倍的也同理，我们可以将这几个测试的基准数据直接判断N与之的余数，如果为0则是合数，否则则为素数。

// 对prime函数添加对2,3,5的判断
bool prime(int n){
	if(n%2==0){return false;}
	if(n%3==0){return false;}
	if(n%5==0){return false;}
	int tmp=sqrt_n(n);
	for (int i = 7; i <= tmp; ++i){
		if(n%i==0)
			return false;
	}
	return true;
}

分析结果：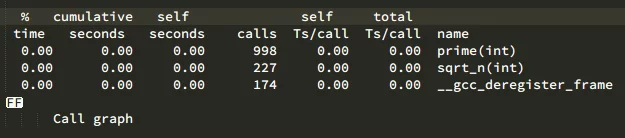

可以看到使sqrt_n的调用降低到了227。

但是，上面的代码在判断上也出现了一些问题：

运行结果：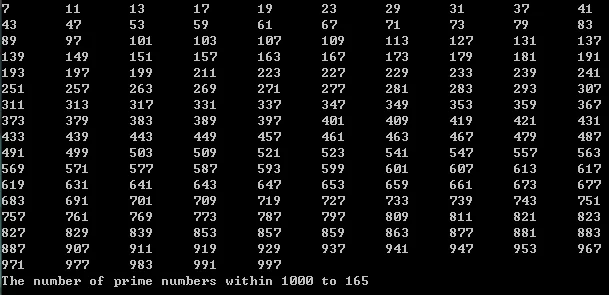

1000以内的素数只找到了165个，但是我们通过穷举所有(第一份代码)，得到的结果是168个。

通过上面的运行结果截图我们能看到2，3，5这三个并没有出现在列表中，因为当n=2，3，5时会导致返回false，所以我们要在代码返回表达式中添加一下判断语句:

// 如果N等于2,3,5就返回true
if(n%2==0){return n==2;}
if(n%3==0){return n==3;}
if(n%5==0){return n==5;}

再次运行：